1. Trashcan selection

In order to further reduce fuel consumption, I can first determine the exigency of a can to be picked as the first thing the program does every day before moving on to running algorithm. As a result, the driver does not need to visit every trashcan every day, if certain cans are not so urgent to be processed. To this end, I use the data recorded by detection sensors to calculate what is called urgency degree to determine the necessity of a bin to be processed today. Then comes to calculation of urgency degree: if it exceeds a predetermined threshold, I mark the can as necessary to be processed today, otherwise don't and leave it until the next day's examination comes. The urgency degree is calculated using equation below:

Urgency Degree = 0.4 × Time + 0.6 × Height
Figure 7 demonstrates 3 trashcans' necessity of being picked up today with premise that the threshold is 61.2. Therefore, the overall process in this step can be summarized in the flowchart below.
Fig.4 Determination of a bin's pickup today

2. Route selection

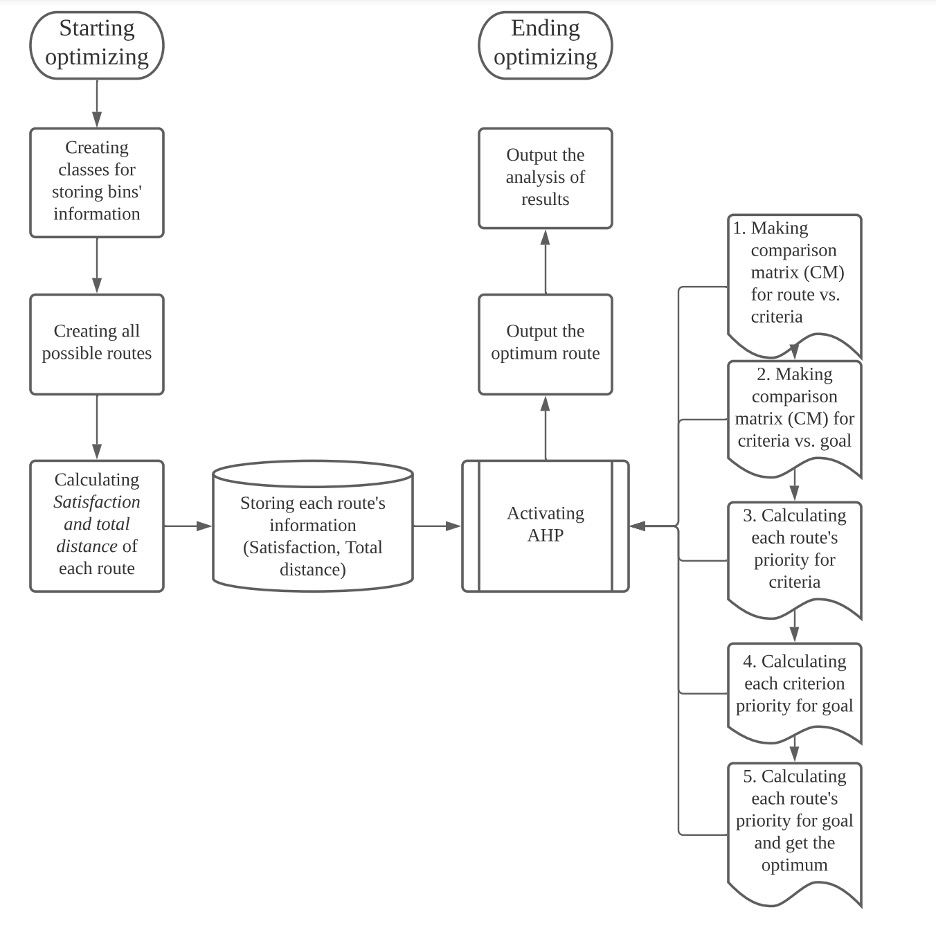
Generally, in singling out the optimal route, there are 7 steps involved: 1) creating classes for storing bins' information; 2) creating all possible routes; 3) calculating satisfaction and total distance of each route; 4) storing each route's information in another class; 5) running AHP; 6) output the optimal route; 7) output the analysis of results. The flowchart describing the overall process is demonstrated in figure 8.

Fig.8 Flowchart of core algorithm

2.1 Producing the initial pool

After knowing trashcans necessary to be processed today, I then have to generate the pool, or all possible routes starting from one trashcan, travelling through all other trashcans, to the final one. Since it is assumed that every two cans have at least one path connecting, I can say every can is connected to all the other ones. As such, permutation is most suitable for producing the pool. For instance, in the case of dealing with 5 waste bins, I can create a list that stores the sequence of visit; namely, [1, 2, 3, 5, 4] means starting from site 1, I sequentially go to site 2, 3, 5, and eventually 4. Thus, I just need to produce all, conclusive variants of this list so that I can have a complete pool of candidates (for now).

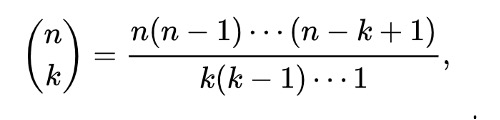
Fig.9 Mathematical formula of permutation

2.2 Completing the pool

Now, holding the pool, I need to create variants further, since every two cans may have more than just one path. Hence, if, say, I are creating variants for a particular sequence list [1, 2, 3, 4, 5], where site 2 and 3 have 3 paths between them, then I can create in total of 3 variants for this sequence list. These variants differ from the original one in total travelled distance, which is one of the factors I consider when deciding the optimal route. I add new variants created from this process to the initial pool. At this point, the pool is completely conclusive and ready for the next step.

2.3 Forming new factor

It is inappropriate to directly take time and height as criteria, since what I are comparing is routes. So, when comparing 2 routes, there is no meaning to compare their time and height. Instead, I can combine the two factors into one more suitable acting as a criterion--Satisfaction. Specifically, in dealing with the case, and the case only, of determining sequence of trashcan to be processed, I know, in fact, the best sequence in the first place when detection sensors record each can's information. Clearly, I want trashcans that are most urgent to get processed to be prioritized, so I can create a standard model according to this fact, where the model is the best sequence starting from the most urgent trashcan to the least. Then, I evaluate the difference between the standard model with each of the routes in the pool. The more they are alike, the higher the satisfaction is.

2.4 Running AHP

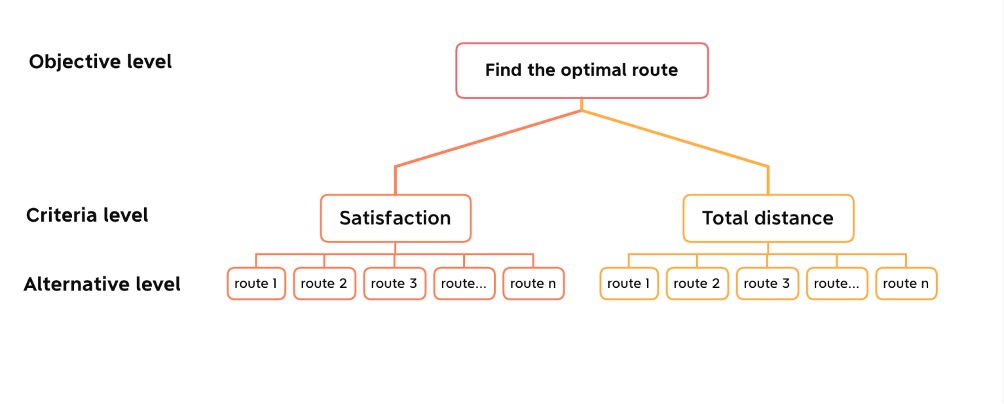
Now I have two criteria when determining the optimal route: satisfaction and total distance. Since our goal is to single out the optimal route among the pool, this is a decision problem. I can construct the problem on 3 levels: objective, criterion, alternative. Therefore, in short, our goal is to determine the best alternative considering all criteria that best meet the objective, as can be shown from figure 9 below.

Fig.10 AHP Hierarchy tree
Analytical Hierarchy Process (AHP) is a perfect solution to coping with such problem. AHP consists of 3 steps: construct the hierarchy tree; create comparison matrix (CM) between objective and criteria and between criteria and alternatives; calculate comparison matrix between objective and alternative. Now that I have built the hierarchy tree, I need to make CM. First of all, objective vs. criteria CM. I have to compare the importance of each criterion under objective, using AHP fundamental scale as figure 10 shown below.
Fig.11 AHP fundamental scale /figcaption>
Since the project's primary goal is to reduce CO2 emission (goal 1), followed by reduction in likelihood of residents facing unpleasant odor produced by kitchen waste (goal 2), I assign 7 to the importance of goal 1 and 1 to that of goal 2. So, goal 1's importance is very strong compared to goal 2's. Then, applying linear algebra, I can calculate priorities of each criterion against the objective. The higher the priority, the more important its corresponding criterion is. Secondly, I create criteria vs. alternatives CM. Every alternative has to be examined in each of criteria. Then, again, I can calculate priorities. Finally, I combine the two kinds of CMs to get the objective vs. alternative CM and calculate each alternative's priority. The alternative with highest priority is the one I are looking for. The process of the core algorithm can be summarized into one flowchart below. Ultimately, I can find the optimal path. Note, however, AHP holds a maximum capacity of routes to be 100, so, when the total candidates exceed 100, I have to make AHP several times, getting Local optimums. Then I process all Local optimums into AHP again to find the Global optimum.

2.5 Analysis of results

Calculation of fuel consumption
The average fuel consumption by pickup truck, in meters per liter, is 2.8 mpg, or 1190.4 meters per liter (APTA, 2019). So, I can divide the total distance of a route by this average to get average fuel consumption during this route.

Calculation of CO2 emission
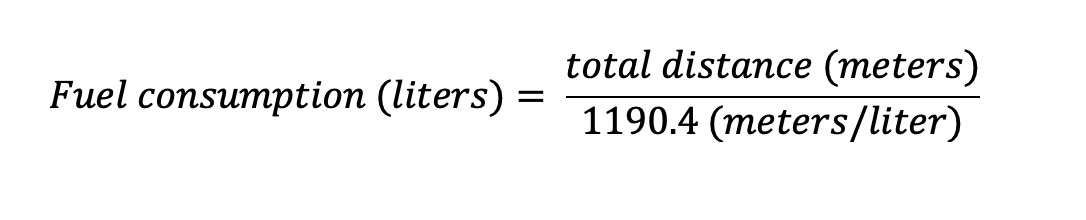
CO2 emission is gained by multiplying the total liters of fuel burned during the route by the average CO2 in one liter. The average CO2 emission per gallon of gasoline is 2347.697 grams (Statista, accessed: Sep 7, 2021).

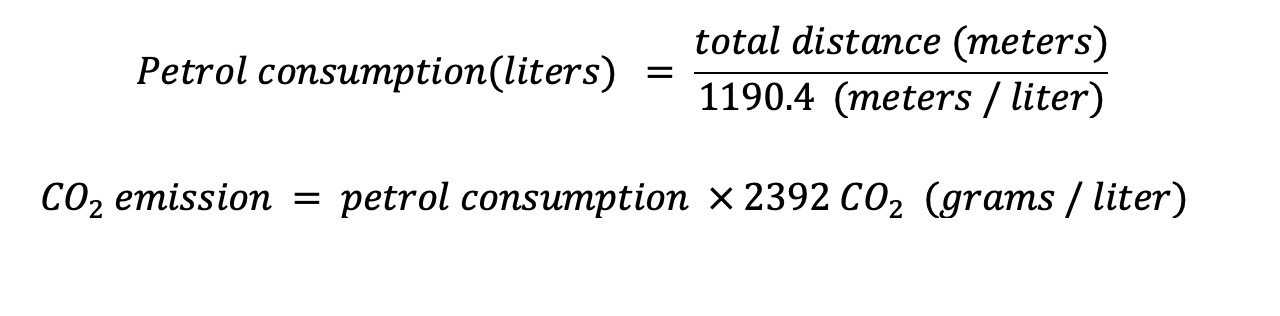
Notes about China's residential abodes
Note, the apartments in China is estimated to 6.45 millions (EPA, accessed: Sep 7, 2021) and I divide it by 5 since I are taking 5 apartments at a time to analyze optimal route amongst them.

2.6 Example of algorithm running in real case

I use an example to illustrate the whole process described above. First of all, I chose 5 apartments, JY, YG, BJ, JK, MW in my district, measured the distance between each two of them, and stored them into a chart.

Since every pair of sites is reversible, meaning disregarding order of the 2 sites, the table does not repeat the distance list given 2 sites when order is reversed. Next, I give random numbers to a trash site's time and height, ranging from 0 to 48 (hrs) and - to 120 (cm) respectively and then calculate their urgency degrees.
Unfortunately, today driver needs to go to every one of trashcans. So, I start generating the initial pool in total of 5 * 4 * 3 * 2 * 1 = 120 routes. Then, according to number of paths between each two trash sites, I produce variants and gain the ultimate pool of routes, waiting for the next move. Processing the pool into AHP, I can finally get the optimal route with its information outputted.